Jun 24, 2021

manim 中的矢量图

了解 Vectorized Math Object

前言

在接触 manim 中的矢量图之前，大家最好先了解一下矢量图这一个概念，以便于更好地理解 manim 对于矢量图的处理方式。

同时，我也在很早以前将这个教程做成了视频，不过一直都没有写博客。视频传送门 BV1364y1y71n

矢量图

网站推荐

介绍

摘自百度百科

矢量图，也称为面向对象的图像或绘图图像，在数学上定义为一系列由点连接的线。矢量文件中的图形元素称为对象。每个对象都是一个自成一体的实体，它具有颜色、形状、轮廓、大小和屏幕位置等属性。

矢量图是根据几何特性来绘制图形，矢量可以是一个点或一条线，矢量图只能靠软件生成，文件占用内在空间较小，因为这种类型的图像文件包含独立的分离图像，可以自由无限制的重新组合。它的特点是放大后图像不会失真，和分辨率无关，适用于图形设计、文字设计和一些标志设计、版式设计等。

如果我们以文本格式打开一个矢量图（以 svg 为例），那么就会看到类似这样的内容¹。

<svg xmlns="http://www.w3.org/2000/svg" version="1.1">
  <path id="lineAB" d="M 100 350 l 150 -300" stroke="red"
  stroke-width="3" fill="none" />
  <path id="lineBC" d="M 250 50 l 150 300" stroke="red"
  stroke-width="3" fill="none" />
  <path d="M 175 200 l 150 0" stroke="green" stroke-width="3"
  fill="none" />
  <path d="M 100 350 q 150 -300 300 0" stroke="blue"
  stroke-width="5" fill="none" />
  <!-- Mark relevant points -->
  <g stroke="black" stroke-width="3" fill="black">
    <circle id="pointA" cx="100" cy="350" r="3" />
    <circle id="pointB" cx="250" cy="50" r="3" />
    <circle id="pointC" cx="400" cy="350" r="3" />
  </g>
  <!-- Label the points -->
  <g font-size="30" font="sans-serif" fill="black" stroke="none"
  text-anchor="middle">
    <text x="100" y="350" dx="-30">A</text>
    <text x="250" y="50" dy="-10">B</text>
    <text x="400" y="350" dx="30">C</text>
  </g>
</svg>

可以看到，文件的内容大致都是坐标，颜色，路径，填充等内容。也正是因为这一个因素，在一些动画软件如 Flash, Animation 中能够对矢量图进行图形的补间操作。而补间的本质，就是插值(interpolate)。这一部分将会在之后的动画模块里面详细阐述。

贝塞尔曲线

网站推荐

介绍

看过上面的几个网站之后，我相信读者对贝塞尔曲线应该有了一定的了解。用文字表述可能相当繁琐： $\displaystyle{ n }$ 条直线顺次相接，每条直线的一端有一个点，让这个点按一定规律从一头移动到另一头，再顺次连接这 $\displaystyle{ n }$ 个点，形成新的 $\displaystyle{ n - 1 }$ 条直线。对接下来的过程进行递归操作，直至只剩一个点时，这个点的运动轨迹。

但是用动画演示相对来说就更好理解了。

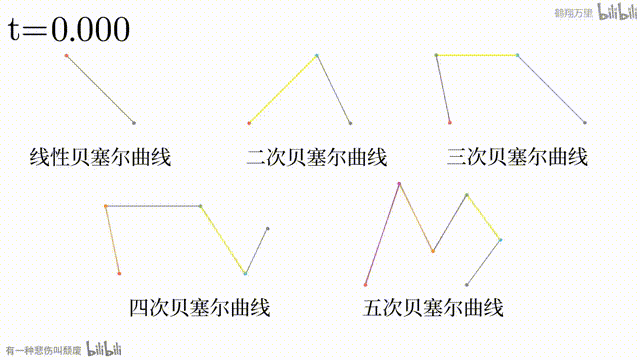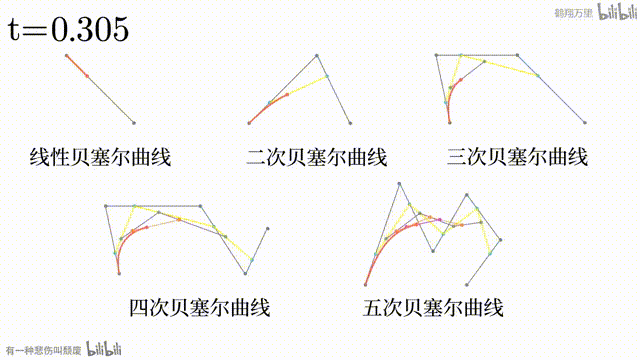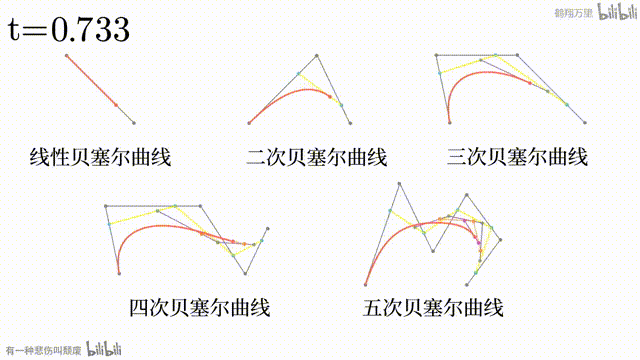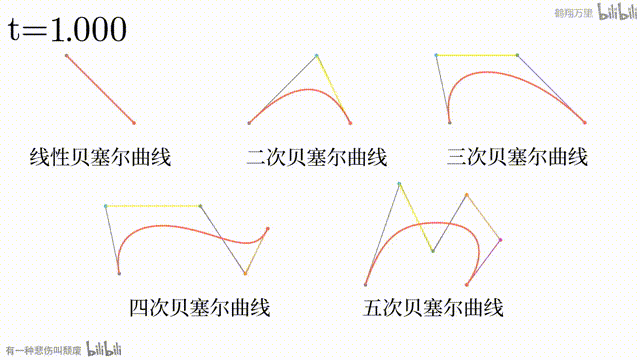
_public/posts-imgs/bez.gif

贝塞尔曲线的一般方程如下，其中 $\displaystyle{ P _{ i } }$ 为创建贝塞尔曲线的 $\displaystyle{ n }$ 个点

\displaystyle{ B \left( t \right) = \sum _{ i = 0 } ^{ n } \left( \begin{array}{c} n \\ i \end{array} \right) P _{ i } \left( 1 - t \right) ^{ i } t ^{ n - i } , t \in \left[ 0 , 1 \right] }

由于贝塞尔曲线可以算是纯靠坐标和计算机运算得到的一种图像，而且它也是构成矢量图的基本元素，因此在本篇中，它是最为核心的要素。

回到矢量图

基于贝塞尔曲线的知识，我们回到 svg 格式的路径，看到 <path> 标签的内容。

下面的命令可用于路径数据²：

M = moveto

L = lineto

H = horizontal lineto

V = vertical lineto

C = curveto

S = smooth curveto

Q = quadratic Bezier curve

T = smooth quadratic Belzier curveto

A = elliptical Arc

Z = closepath

我们顺着继续看一些绘制曲线的例子，其中，螺旋的例子是比较瞩目的，因为他没有使用原生的矩形、椭圆等工具来绘制，而是纯路径绘制。

这里出现了我们的老朋友贝塞尔曲线。如果我们打开一个由 manim 生成的 Text 的 svg 文件，那么就会看到有大量的 C x1 y1 x2 y2 x3 y3，这就对应了二阶贝塞尔曲线中的三个二维坐标，回到上面的动图，看一眼它的生成过程，再体会一下用很多段二阶贝塞尔曲线拼接成一段完整的路径。

manim 中的矢量图

Vectorized Math Object

没错，就是这个非常神奇的类 VMobject，它就是所有平面几何图形和文字的父类。下面给出它的部分成员变量和方法。由于其中还涉及到关于上色、变换等元素，在这里只呈现部分与锚点相关的内容。

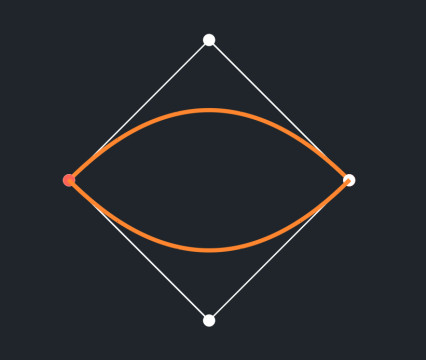
## 此处的 VMobject 为 manimgl 最新版
class VMobject(Mobject):
    CONFIG = {
        "fill_color": None,                    ## 填充色
        "fill_opacity": 0.0,                   ## 填充色透明度
        "stroke_color": None,                  ## 轮廓颜色
        "stroke_opacity": 1.0,                 ## 轮廓透明度
        "stroke_width": DEFAULT_STROKE_WIDTH,  ## 轮廓线宽
        ...,
        "n_points_per_curve": 3,               ## 每条贝塞尔曲线由 3 个点构成
        ...
    }
    ...
    def init_data(self):
        self.data = {
            "points": np.zeros((0, 3)),
            "bounding_box": np.zeros((3, 3)),
            "rgbas": np.zeros((1, 4)),
        }                                      ## 此处原本调用父类的方法，这里将方法补充完整
        self.data.pop("rgbas")
        self.data.update({
            "fill_rgba": np.zeros((1, 4)),
            "stroke_rgba": np.zeros((1, 4)),
            "stroke_width": np.zeros((1, 1)),
            "unit_normal": np.zeros((1, 3))
        })                                     ## 对于 VMobject 的上色方案进行了重写
    ...

其中，n_points_per_curve 指示了一条贝塞尔曲线由 3 个锚点构成，而 VMobject 这个类允许用多条贝塞尔曲线来构成一系列的图形。我们可以使用 vmob.set_points([...]) 方法来设置它的形状。列表中放了所有构成这个图形的锚点，它的长度必须是 3 的倍数。下面给出一个例子，能够画出一个橄榄形。

v = VMobject()
v.set_points(np.array([
    [-2, 0, 0], [0, 2, 0], [2, 0, 0],
    [2, 0, 0], [0, -2, 0], [-2, 0, 0]
]))

_public/posts-imgs/olive.jpg

而其本质就是将两段贝塞尔拼接起来。下图即为加上锚点和手柄的图像。

_public/posts-imgs/olive-withhandle.jpg

为何使用二阶贝塞尔

在旧版的 manim-cairo 中用的是三阶贝塞尔，新版 manimgl 中为二阶贝塞尔，本质区别不大。但肯定会有人好奇为什么可以用更高阶的贝塞尔曲线却不用。原因就在于贝塞尔曲线的参数方程 ~~再放送~~

$B(t)=\sum_{i=0}^{n}\binom{n}{i}P_{i}(1-t)^{i}t^{n-i},t\in[0,1]$

我们可以看到这其中包含了组合数，而组合数的运算包含了阶乘，这一运算符相对来说复杂度是比较高的。而虽然高阶贝塞尔曲线的方程可以通过使用递归，分解为一个个低阶数的来构成，但我们知道递归的复杂度在这种情况下会指数上升，在这里使用递归运算的速度可能还真的不如直接代数运算。

为了尽可能的降低运算的复杂度，人们就采用了低阶数的贝塞尔来拼接成一段完整的路径。从 w3school 的最后一个例子中，可以看到在 svg 的路径中也采用了多段二阶贝塞尔拼接成完整路径的方法。

从抽象到具象

从前面的基础知识到现在，终于可以讲一些具体的几何图形了。

如果大家翻过 geometry.py 文件的源码，可以发现不少几何图形都调用了父类 VMobject 的方法，例如 set_points_as_corners, add_line_to, close_path 等等，这些从方法名就基本上能看懂是什么意思，也可以阅读源码来理解它的运作方式。

曾有人说，直线就是不够弯的曲线。那么在 manim 中，直线就可以用 3 个在直线上均匀分布的锚点来构成。为什么说要均匀分布呢？虽然分布不均匀也可以构成直线，最多也不过加了一点拉扯，但为了运算方便，同时也为了减少 bug，在处理时就将这 3 个锚点等距的放在一条线上。

_public/posts-imgs/line.png

关于在三个点在同一直线上拉扯的问题

在测试中，也出现了这样的 bug，发生原因大致是 shaders 上色之前使用了 interpolate 对坐标、颜色等属性进行了补间，导致出现了一些偏差。

使用下面的代码，会发现直线的粗细会有一些问题，甚至出现断裂。

图中数字为锚点的位置和编号。

v = VMobject()
v.set_points(np.array([[-1, 0, 0], [3, 0, 0], [1, 0, 0]]))

_public/posts-imgs/problem-of-handle.jpg

从直线到曲线

在刚刚贝塞尔曲线的介绍中，我们了解到了二阶贝塞尔拥有两个锚点，分别控制起点和终点，而还有一个手柄，可以控制曲线的弯曲程度。其中，圆弧就是通过这一方法来构成的，我们可以看一下圆弧类的一个静态方法，这个方法就是用来计算构成圆弧的一系列锚点的。在代码之后会放一段流程图说明其构造过程。

@staticmethod
def create_quadratic_bezier_points(angle, start_angle=0, n_components=8):
    ## n_components 表示一条圆弧用 8 条二阶贝塞尔曲线构成
    ## 从圆弧的开始到终止构造 17 个点
    samples = np.array([
        [np.cos(a), np.sin(a), 0]
        for a in np.linspace(
            start_angle,
            start_angle + angle,
            2 * n_components + 1,
        )
    ])
    ## 将圆弧的圆心角等分为 8 份，分别用贝塞尔曲线拟合
    theta = angle / n_components
    ## 将下标为奇数的点移动到偶数点处作切线相邻两者相交处
    samples[1::2] /= np.cos(theta / 2)

    ## 创建八条贝塞尔曲线的锚点
    points = np.zeros((3 * n_components, 3))
    points[0::3] = samples[0:-1:2]
    points[1::3] = samples[1::2]
    points[2::3] = samples[2::2]
    return points

_public/posts-imgs/arc.gif

函数图像曲线

在 manimlib/mobject/funcions.py 中，可以看到 ParametricCurve 这个类。它的意思本来是参数方程，但是它也可以用来画 $\displaystyle{ y = f \left( x \right) }$ 的方程。FunctionGraph 就是继承它得到的。

从这个类的 init_points 方法中，我们可以大致的猜到，函数曲线是将定义域细分为很多个小段，在每一个小段上都对图像进行拟合，这里的拟合依然是用了一条二阶贝塞尔。在一定程度上分的越细，拟合的就越精确。

函数曲线的构建过程中还涉及到了使曲线变平滑的一些方法，博主目前还没有学到，因此在这里不过多的阐述。主要的一些方法有

change_anchor_mode
make_smooth
make_approximately_smooth
make_jagged

文字

旧版的 manim 采用 cairo 库生成文字并将其转换为 svg 路径，而新版因为抛弃了 cairo 绘图，因此顺便也将 cairo 生成文字也抛弃了，使用了 Manim Community 开发的 ManimPango 库。

在矢量图的部分也提到了，路径大多是由很多段贝塞尔曲线拼接而成的，文字 svg 也不例外，而且恰好它们大多也都是二阶贝塞尔，与 manimgl 的矢量图相匹配。 ~~虽然现在文字的填充有时候还是会因为三角剖分的问题而变得鬼畜。~~ 那么，现在就可以把文字当作是一个几何图形来看待了，有轮廓，有填充色，能够进行变换。

矢量图的变换

从开头到现在，我们提到的能够直接构成矢量图形的只有贝塞尔曲线，而决定贝塞尔曲线的就是它的锚点。我们只需要对锚点进行坐标变换，就可以从最底层的方面来影响其表象了。

例如 scale 方法，无非就是将构成矢量图的所有点的坐标乘上一个数，如果有 about_point 参数，那就只是加一个相对坐标的运算罢了。

如果再复杂一些，例如在 $\mathbb{R}^3$ 空间的变换，只要你的数学足够好，那应当就不会有太大的问题，在 example_scenes.py 中 Grant 给出了一些例子，读者可以去研究一下。在 VMobject 中已经给出的一些变换方法如下

apply_function
apply_points_function
apply_complex_function
···

矢量图的组合

VGroup

VGroup 类继承于 VMobject，不过它本身也可以作为一个容器，也就是说我们可以把它当作一个列表来看待，使用 add 和 remove 方法添加或删除元素，也可以通过方括号下标来进行索引。但是 VGroup 对于图层的适配是相当差的（其实 manim 本身就对图层适配很差）。

append_points

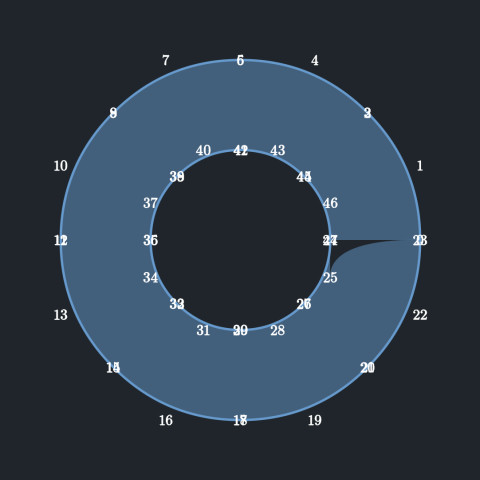
在 VMobject 中有一个方法 reverse_points，作用是将锚点反转。听上去这个反转好像并没有什么卵用，但实际上还是有不少使用例的，Annulus 环形实际上就是由两个相反的圆组合而成的。下面给出它的定义。

class Annulus(Circle):
    CONFIG = {
        "inner_radius": 1,
        "outer_radius": 2,
        "fill_opacity": 1,
        "stroke_width": 0,
        "color": WHITE,
        "mark_paths_closed": False,
    }

    def init_points(self):
        self.radius = self.outer_radius
        outer_circle = Circle(radius=self.outer_radius)
        inner_circle = Circle(radius=self.inner_radius)
        inner_circle.reverse_points()
        self.append_points(outer_circle.get_points())
        self.append_points(inner_circle.get_points())
        self.shift(self.arc_center)

可以看到，它的创建过程其实也相当简单，就是将内圆的点集反转，附加到外圆的点集中，再加上填充色，就变成圆环了。

为什么它会填充成一个圆环，而不是两次都向内填充呢？

可以这么思考：圆的一圈点集，是按照逆时针分布的，那么这条路径也可以看作是有向的，而上色机制会将向量的左边进行填充。将内圈的圆点集反转，那么路径方向也会反转，而上色机制同样对向量的左边进行填充。两者同时成立，得到的就是外圆扣去内圆的形状了。~~请忽略填充不完整的 bug~~

_public/posts-imgs/annulus.jpg

总结

本篇主要阐述了在 manim 中如何通过控制锚点来创建自定义物件（当然仅限于矢量图），用贝塞尔曲线来拟合图像的一些过程。总之就是通过修改底层（DNA）来控制表象（相对性状）~~什么玩意居然在这里扯生物~~。

如何显示锚点的位置和索引，可以自定义一个类，代码在这里给出。

class AllPointsIndex(VGroup):
    CONFIG = {
        "scale_factor": 0.5,
        "color": WHITE,
    }
    def __init__(self, obj, **kwargs):
        ## digest_config(self, kwargs)
        VGroup.__init__(self, **kwargs)
        for index, points in enumerate(obj.get_all_points()):
            point_id = Integer(index, background_stroke_width=2) \
                .scale(self.scale_factor).set_color(self.color)
            point_id.move_to(points)
            self.add(point_id)

菜鸟教程，详见 https://www.runoob.com/svg/svg-path.html ↩
w3school, https://www.w3school.com.cn/svg/svg_path.asp ↩

#manim #教程 #矢量图

manim 中的矢量图

前言

矢量图

网站推荐

介绍

贝塞尔曲线

网站推荐

介绍

回到矢量图

manim 中的矢量图

Vectorized Math Object

为何使用二阶贝塞尔

从抽象到具象

从直线到曲线

函数图像曲线

文字

矢量图的变换

矢量图的组合

VGroup

append_points

总结

Footnotes