Jul 3, 2022

updater 文档 | 第 4 节 Alpha 在动画中的作用

碎碎念

如果是看过我 B 站视频的同学，应该会发现我把这部分顺序稍微调整了一下，但其实也无伤大雅，毕竟一旦想学会使用 updater ，那么就必然需要阅读源码，而这部分文档实际上就是带领读者去阅读 manim 源码，了解动画的工作原理。

前面我们也常常提到一个词叫做插值，它的泛型一般定义成这样

def interpolate(start: T, end: T, alpha: float) -> T:
    return (1. - alpha) * start + alpha * end

我们前面也没有去提到过多关于 alpha 的内容，这一节将会尝试讲解这一困惑。

Alpha 的含义

可能我们在图像处理的时候听说过一个 “alpha 通道” 的概念，其实就是指透明度通道。而它的取值范围是 0%~100%，也就是 $\displaystyle{ \left[ 0 , 1 \right] }$ 。

如果我们尝试将这个值代入到上面的函数定义中，发现它返回的是 start 与 end 之间的一个中间值。而补全中间值其实就是补间动画的一个重要任务了，它让画面的切换变得看起来更加平滑，而不会非常生硬。

我们再拿出之前的一张图，在动画的过程中，alpha 的值从 0 到 1 变化，而图形也由原来的方形变得越来越像变化之后的圆形。

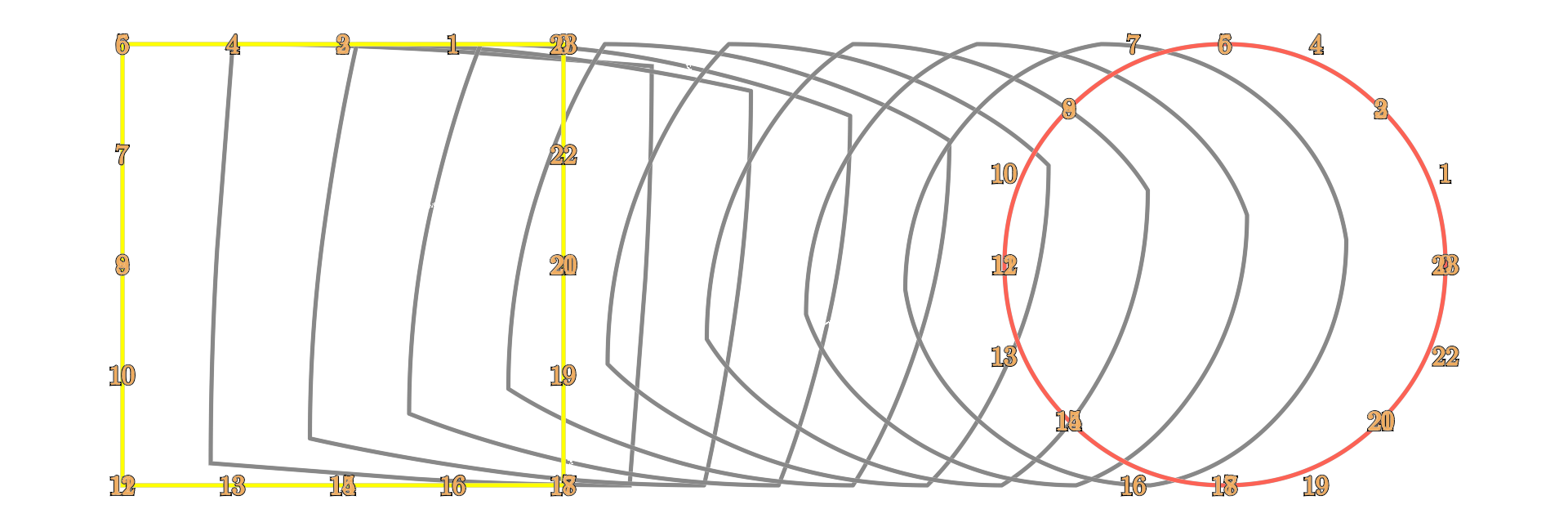
_public/updater/InterpolateExampleScene.png

在这里，alpha 所做的就是在 $\displaystyle{ \left[ 0 , 1 \right] }$ 定义域上，对于每个选到的值，算出对应的物件状态。

至于为什么是选到的值，这就要聊聊视频这一概念了。我们都知道，视频有一个叫做帧率的属性，它代表着每一秒钟，视频会播放多少个画面。由于计算机的算力、硬盘的存储容量均有限，我们不可能用有限的事物来存储和计算无限的、连续的现实世界，只能尽可能的去保存一些离散的数据，在视频播放的过程中，尝试利用人眼的视觉暂留，骗过人类，让我们认为这是连续的。而对于 60 帧的视频，我们只需每秒让计算机算出 60 个 alpha 值分别对应的状态，即可生成视频。

graph LR a["连续的 alpha ∈ [0,1]"] --"离散采样"--> b["离散的一系列 alpha
每秒 60 个离散值"] b --"计算画面"--> c["离散的一系列画面
每秒 60 张"]

%%{init: {'theme':'dark'}}%% graph LR a["连续的 alpha ∈ [0,1]"] --"离散采样"--> b["离散的一系列 alpha
每秒 60 个离散值"] b --"计算画面"--> c["离散的一系列画面
每秒 60 张"]

动画的执行流程

我们再回忆一下第 1 节的内容，Animation 类编写了很多方法，在 Scene 调用 play 的时候，会按一定的顺序和逻辑去调用 Animation 的这些方法。此时我们关注的就是其中实际的动画部分了。

def progress_through_animations(self, animations: Iterable[Animation]) -> None:
    last_t = 0
    for t in self.get_animation_time_progression(animations):
        dt = t - last_t
        last_t = t
        for animation in animations:
            animation.update_mobjects(dt)
            alpha = t / animation.run_time
            # 动画插值
            animation.interpolate(alpha)
        self.update_frame(dt)
        self.emit_frame()

Animation 的方法方法一层套一层，最终会到达 interpolate_mobject 和 interpolate_submobject 这两个方法身上。我们来看 manim 中最常用的方法 Transform ，它是怎么实现的：

    def interpolate_submobject(
        self,
        submob: Mobject,
        start: Mobject,
        target_copy: Mobject,
        alpha: float
    ):
        submob.interpolate(start, target_copy, alpha, self.path_func)
        return self

没错，要做的事情就只有一行！从中应该可以想象到 Transform 的实现有多么简单粗暴，只需要使得在屏幕上的物件成为起始和目标的中间值就可以了。

其实这么一来，许多工作就落到了 begin 和 finish 头上。它们要完成的工作，包括检查合法性、对齐起始物件和目标物件的数据、以及一些优化问题。

其中，第二个步骤应当是在运行进程中比较关键的步骤。不妨假设有下面这个例子：

给定两个任意矩阵，尝试给出这两个矩阵的 0.5 处的插值

这么听的确是强人所难，如果两个矩阵不一样大，那么根本就不可能进行插值。

在这一过程中，数据对齐的作用就显得相当重要了。如果我们把这两个矩阵都进行扩展，使得新的矩阵大小都能覆盖两个矩阵，接着对一些缺失的数据进行修补，那么此时一个矩阵中的每一个值都能与另一个矩阵中的相应值形成一一映射，这样插值动画就可以畅通无阻了。

_public/updater/MatrixReflect.png

graph LR begin -->a["检查"] --> b["数据对齐"] --> c["拷贝变量"] c --> d["lock data
优化"] --> e["插值
interpolate
mobject"] e --> f["unlock data"] --> g["finish"]

%%{init: {'theme':'dark'}}%% graph LR begin -->a["检查"] --> b["数据对齐"] --> c["拷贝变量"] c --> d["lock data
优化"] --> e["插值
interpolate
mobject"] e --> f["unlock data"] --> g["finish"]

UpdateFromAlphaFunc

讲了那么多前置知识，终于能将这一节的重点了。这个动画类其实类似于向我们暴露了一个接口，让我们来动手实现这个动画的具体流程。

而在源码层面上，这个类继承于 Animation ，接收的参数有两个：一个是 mobject ，另一个是更新函数。而待我们实现的更新函数，就是物件更新的依据。而事实上也就是让我们直接实现 interpolate_mobject 方法。越是接近底层，其灵活度也就越高。

class UpdateFromAlphaFunc(Animation):

    def __init__(
        self,
        mobject: Mobject,
        update_function: Callable[[Mobject]],
        **kwargs
    ):
        self.update_function = update_function
        super().__init__(mobject, **kwargs)

    def interpolate_mobject(self, alpha: float) -> None:
        self.update_function(self.mobject, alpha)

用这一个动画类我们几乎可以实现任何效果，只需要计算出 alpha 值对应的物件状态，就可以实现我们想要的动画了。

Caution

在 1.6.1 及以后的某些版本，restore 方法可能存在 bug ，导致有些效果都没有办法还原出来。

我们可以在每一帧都恢复初态、重新计算当前状态、提交，这样来控制其实更加方便。例如下面一个旋转平移的效果（但是笔者当前版本是 1.6.1 之后的，却没有出现问题）

class ShiftRotateExample(Scene):
    def construct(self):
        square = VGroup(Square(), Dot()).shift(LEFT*5)
        numline = NumberLine(x_range=[-5, 5, 1])

        # 保存初态
        square.save_state()

        def anim(m: Mobject, alpha: float):
            # 恢复初态
            m.restore()
            # 移动
            m.shift(10 * alpha * RIGHT)
            # 旋转
            m.rotate(PI * 3 * alpha)

        self.add(numline, square)
        self.play(UpdateFromAlphaFunc(square, anim), run_time=4)

既然这样稍微复杂一些的动画效果可以用 UpdateFromAlphaFunc 实现，那么我们就用它来实现一个 MyRotate 吧！

尝试编写一个函数，当传入 UpdateFromAlphaFunc 时，能达到旋转的效果

class MyRotateExample(Scene):
    def construct(self):
        square = Square()
        # 保存初态
        square.save_state()

        def my_rotate(m: Mobject, alpha: float):
            # 恢复初态
            m.restore()
            # 旋转
            m.rotate(PI * 3 * alpha)

        self.add(square)
        self.play(UpdateFromAlphaFunc(square, my_rotate), run_time=4)

Alpha 还能在哪里找到——Bézier Curve

如果阅读过笔者以前的博客，应该都知道 manim 中一切皆为 Mobject ，而它又有一个重要的子类 VMobject ，它的本质是贝塞尔曲线。而提到贝塞尔曲线，就不得不提到其生成原理：插值。

manim 的作者考虑的很周全，为了避免计算高阶贝塞尔曲线，提高运算性能，他使用许多段短曲线拼接成完整的复杂曲线。尽管在宏观上好像抛弃了 $\displaystyle{ n }$ 阶贝塞尔曲线完整定义，“似乎”没有办法去利用它这个 alpha 了，但是 VMobject 依然实现了一个曲线采样方法：point_from_proportion，简写为 pfp 。

这个方法应该常用于函数曲线，向其中传入一个百分比 alpha ，范围是 $\displaystyle{ \left[ 0 , 1 \right] }$ ；输出值是一个点的坐标，而这个点位置在曲线长度百分比 alpha 处。（~~一直感觉没有办法很好地表述这段话~~）

绘制一条曲线，并在上面取一个点，让点从曲线的起始位置，顺着曲线移动到结束位置。

class MoveAlongPathExample(Scene):
    def construct(self):
        graph = FunctionGraph(lambda x: np.sin(PI * x),
                              x_range=[-5, 5, 0.1])
        self.add(graph)

        dot = Dot().move_to(graph.get_start())
        self.add(dot)

        def update_dot(dot: Mobject, alpha: float):
            dot.move_to(graph.pfp(alpha))

        self.play(UpdateFromAlphaFunc(dot, update_dot), run_time=4)

然而，Grant 早就已经封装好一个动画类了，叫 MoveAlongPath ，感兴趣的读者可以尝试一下。

接下来加大一点难度。

绘制一条曲线，在上面取一个点，在这个点处绘制一个小箭头，使得这个箭头顺着曲线移动的时候，朝向永远顺着曲线的切线方向。小箭头可以使用 ArrowTip 代替 Dot 。

# 计算输入 alpha 对应点处切线的倾斜角
def angle_of_tan(graph: ParametricCurve, alpha: float, dx=0.01) -> float:
    vect = graph.pfp(alpha + dx) - graph.pfp(alpha - dx)
    return angle_of_vector(vect)

class MoveAlongPathExample2(Scene):
    def construct(self):
        graph = FunctionGraph(lambda x: x * np.cos(PI * x) / 2,
                              x_range=[-5, 5, 0.1])
        arrow = ArrowTip().scale(0.8)
        # 保存 arrow 的旋转角度
        arrow.save_state()
        self.add(graph, arrow)

        def update_arrow(m: Mobject, alpha: float):
            # 恢复到初态，主要是为了恢复旋转角
            m.restore()
            # 旋转
            m.rotate(angle_of_tan(graph, alpha))
            # 移动
            m.move_to(graph.pfp(alpha))

        self.play(UpdateFromAlphaFunc(arrow, update_arrow), run_time=6)

UpdateFromFunc

从这个类的名字来看，其实就是无需传入 alpha 的动画更新。但是没有了 alpha ，也就无法构成动画，因此这个方法常常作为伴随动画，用作某一段时间内动画的附加效果。

例如，我们想让点移动的时候，文本保持在它的旁边，但是我们不使用 add_updater 方法，此时就可以使用 UpdateFromFunc 作为一个伴随效果，添加到 play 中。

self.play(
    dot.animate.shift(RIGHT * 2),
    UpdateFromFunc(text, lambda m: m.next_to(dot))
)

由于这个方法无法使用 alpha 参数，因此限制也是非常多，基本上也就只能作为伴随动画了。

更多的例子

1. 2022-07-01 版本中， manimgl 自带样例中 CoordinateSystemExample 因为使用 always_redraw 坏掉了，究其原因是 updater 和 become 的冲突问题。现在请你尝试抛弃前面的方法，用 UpdateFromFunc 和 become 来修复它。

参考解答

# 重绘坐标线
def redraw_h_line(m: Mobject):
    m.become(axes.get_h_line(dot.get_left()))

def redraw_v_line(m: Mobject):
    m.become(axes.get_v_line(dot.get_bottom()))

self.play(
    ShowCreation(h_line),
    ShowCreation(v_line),
)
self.play(
    dot.animate.move_to(axes.c2p(3, -2)),
    # UpdateFromFunc 作为伴随动画，下同
    UpdateFromFunc(h_line, redraw_h_line),
    UpdateFromFunc(v_line, redraw_v_line)
)
self.wait()
self.play(
    dot.animate.move_to(axes.c2p(1, 1)),
    UpdateFromFunc(h_line, redraw_h_line),
    UpdateFromFunc(v_line, redraw_v_line)
)
self.wait()

f_always(dot.move_to, lambda: axes.c2p(1, 1))
self.play(
    axes.animate.scale(0.75).to_corner(UL),
    UpdateFromFunc(h_line, redraw_h_line),
    UpdateFromFunc(v_line, redraw_v_line),
    run_time=2,
)

这么写下来发现真的好烦， updater + become 真的是万能，但是有 bug

2. 编写一个半径为 1 的圆在半径为 2 的圆上滚动一周的动画，并使用 TracedPath 来绘制起始两圆切点在动画中的轨迹。为了更清楚地看出圆的旋转角度，可以添加一个由圆心指向初始切点的箭头。

如果使用 UpdateFromAlphaFunc ，那么旋转的角度、半径需要手动计算后写入。

参考解答

class RollingCircleExample(Scene):
    def construct(self):
        c1 = Circle(radius=2)
        c2 = VGroup(
            Circle(radius=1),   # 圆
            Dot(),              # 圆心
            Vector(DOWN * 0.8), # 箭头
        )
        c2.shift(UP * 3).set_color(GOLD)
        c2.save_state()

        path = TracedPath(lambda: c2[0].pfp(0.75), # 圆的 3/4 处坐标
                          stroke_width=6,
                          stroke_color=YELLOW)

        self.add(c1, c2, path)

        def update_c2(m: Mobject, alpha: float):
            m.restore()
            m.rotate(-3 * TAU * alpha)
            m.move_to(3 * np.array([
                np.sin(TAU * alpha),
                np.cos(TAU * alpha),
                0
            ]))

        self.play(
            UpdateFromAlphaFunc(c2, update_c2),
            run_time=6
        )

3. 给定三个锚点，用贝塞尔曲线的定义来绘制这三个点生成的曲线。

参考解答

class BezierExample(Scene):
    def construct(self):
        points = np.array([
            [-4, -3, 0],
            [0, 3, 0],
            [6, -2, 0]
        ])

        dots = VGroup(*[Dot(p) for p in points])
        lines = VGroup(
            Line(points[0], points[1]),
            Line(points[1], points[2]),
        ).set_stroke(width=2)

        self.add(dots, lines)

        moving_dot1 = Dot(points[0], color=GOLD)
        moving_dot2 = Dot(points[1], color=GOLD)

        moving_line = Line(points[0], points[1], color=GOLD)

        moving_line.add_updater(
            lambda l: l.put_start_and_end_on(
                moving_dot1.get_center(),
                moving_dot2.get_center()
            )
        )

        moving_dot3 = Dot(color=RED)

        path = TracedPath(moving_dot3.get_center, stroke_width=6, stroke_color=RED)

        self.add(moving_dot1, moving_dot2, moving_dot3, moving_line, path)

        self.play(
            UpdateFromAlphaFunc(moving_dot1, lambda d, a: d.move_to(lines[0].pfp(a))),
            UpdateFromAlphaFunc(moving_dot2, lambda d, a: d.move_to(lines[1].pfp(a))),
            UpdateFromAlphaFunc(moving_dot3, lambda d, a: d.move_to(moving_line.pfp(a))),
            run_time=4
        )

#manim #updater #教程